Trie

Trie is an efficient information reTrieval data structre (especially for string), which supports serach, insert and delete operations. Maximum number of children of a node is equal to size of alphabet. Using Trie, search complexities can be brought to optimal limit (key length).

Advanteges:

1. Insert and find string with lower time complexity $O(L)$, where $L$ is the length of a single word.
2. Efficiently do prefix search.

   Issues:

3. A lot of memory requirement for storing the strings.

The final conclusion regarding tries data structure is that they are fast but require huge memory for storing the strings.

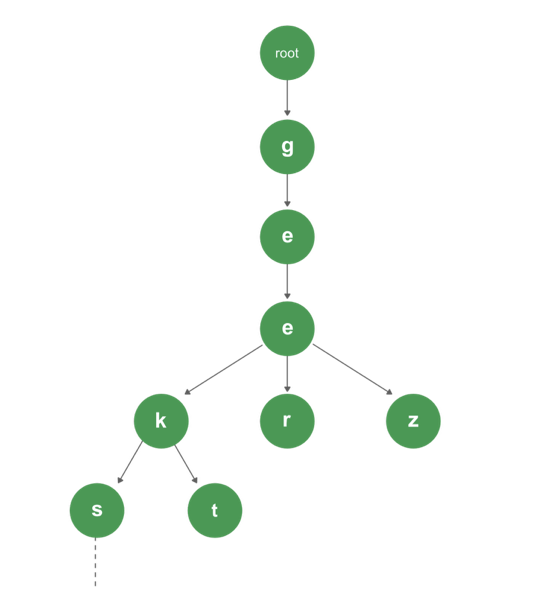
Trie Node

// Trie Node
struct TrieNode {
    struct TrieNode* children[ALPHABET_SIZE];
    // isEndOfWord is true iff the node represents end of a word
    bool isEndOfWord;
}

Insertion

Inserting a key into Trie is a simple approach. Every character of the input key is inserted as an individual Trie node.
If the input key is new or an extension of the existing key, we need to construct non-existing nodes of the key, and mark end of the word for the last node.
If the input key is a prefix of the existing key in the Trie, we simply mark the last node of the key as the end of a word.

// If not present, inserts key into trie
// If the key is prefix of trie node, just
// marks leaf node
void insert(struct TrieNode* root, string key)
{
    struct TrieNode* pCrawl = root;

    for (int i = 0; i < key.length(); i++) {
        int index = key[i] - 'a';
        if (!pCrawl->children[index])
            pCrawl->children[index] = getNode();

        pCrawl = pCrawl->children[index];
    }

    // mark last node as leaf
    pCrawl->isEndOfWord = true;
}

Search

The search is similar to insert operation. The serach can terminate due to the end of a string of lack of key in the trie.
In the former case. if the isEndOfWord field of the last node is true, then the key exists in the Trie.
In the second case, if the search terminates without examining all the characters of the key, since the key is not present in the Trie.

// Returns true if key presents in trie, else
// false
bool search(struct TrieNode* root, string key) {
    struct TrieNode* pCrawl = root;
    for (int i = 0; i < key.length(); i++) {
        int index = key[i] - 'a';
        if (!pCrawl->children[index])
            return false;

        pCrawl = pCrawl->children[index];
    }
    return (pCrawl != NULL && pCrawl->isEndOfWord);
}

Deletion

The possible conditions:

1. Key may not be there in Trie.
2. Key present as unique key. Delete all the nodes.
3. Key is a prefix key of another long key in Trie. Unmark the leaf node.
4. Key has at least one othe key as prefix key. Delete nodes from end of key until first leaf node of the longest prefix key.

   // Returns true if root has no children, else false
   bool isEmpty(TrieNode* root) {
       for (int i = 0; i < ALPHABET_SIZE; i++)
           if (root->children[i])
               return false;
       return true;
   }
   // Recursive function to delete a key from given Trie
   TrieNode* remove(TrieNode* root, string key, int depth = 0) {
       // If tree is empty
       if (!root)
           return NULL;
       // If last character of key is being processed
       if (depth == key.size()) {
           // This node is no more end of word after
           // removal of given key
           if (root->isEndOfWord)
               root->isEndOfWord = false;
           // If given is not prefix of any other word
           if (isEmpty(root)) {
               delete (root);
               root = NULL;
           }
           return root;
       }
       // If not last character, recur for the child
       // obtained using ASCII value
       int index = key[depth] - 'a';
       root->children[index] =
             remove(root->children[index], key, depth + 1);
       // If root does not have any child (its only child got
       // deleted), and it is not end of another word.
       if (isEmpty(root) && root->isEndOfWord == false) {
           delete (root);
           root = NULL;
       }
       return root;
   }