To calculate the longest palindrome substring.
Algorihtm
- preprocessing
insert ‘#’ between adjacent characters in the string, e.g., babad $\rightarrow$ #b#a#b#a#d#.
remark: after preprocessing, the length of the string after and the length of the palindrome substring is odd. - array P
P[i]: The maximum extension length of the palindrome substring centered on the i-th character.
For example: abbabb
- calculate P with previous information.
maxRight: the rightmost boundray.center: the center correpsonds to maxRight.- case 1: $i \ge {\rm maxRight}$
extend at the i-th character to enlarge maxRight. - case 2: $i < {\rm maxRight}$
find mirror which is symmetric with $i$ about center, i.e., ${\rm mirror} + i = 2\times {\rm center}$.- ${\rm P}[{\rm mirror}] < {\rm maxRight} - i$, which means that ${\rm P}[i] = {\rm P}[{\rm mirror}]$.
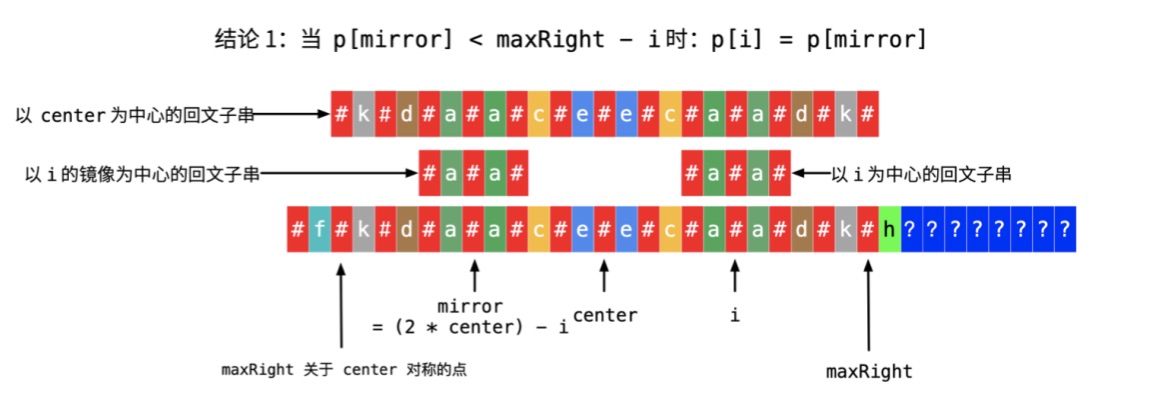
- ${\rm P}[{\rm mirror}] = {\rm maxRight} - i$, which means that ${]rm P}[i]$ is at least ${\rm maxRight} - i$ and may be extended.
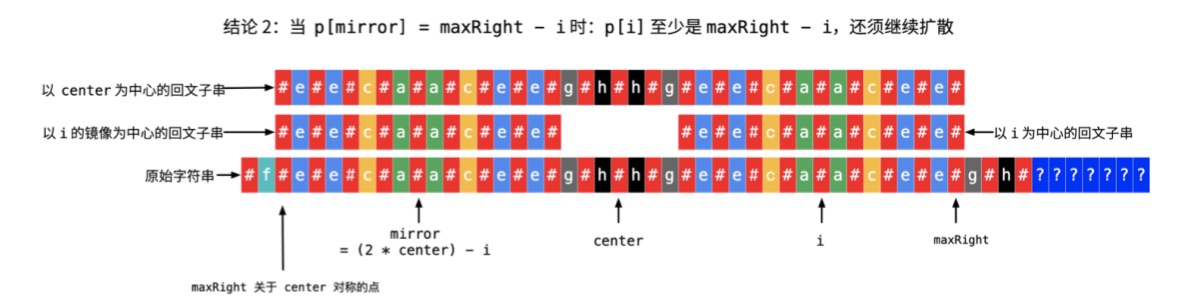
- ${\rm P}[{\rm mirror}] < {\rm maxRight} - i$, which means ${\rm P}[i] = {\rm maxRight} - i$ and can not be extended.
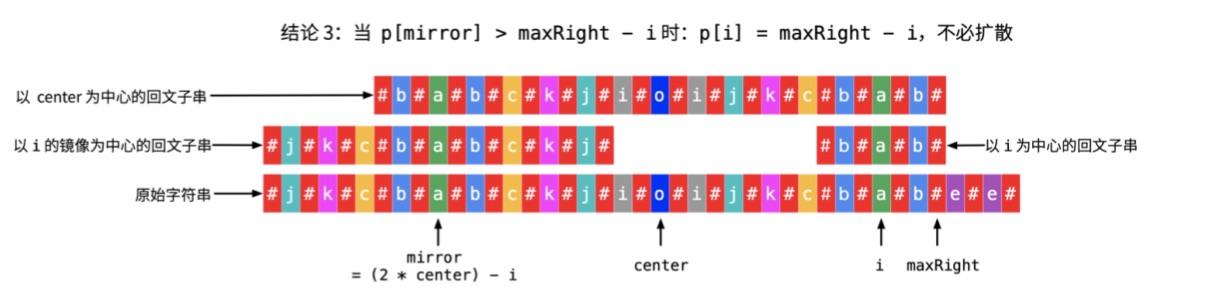
- ${\rm P}[{\rm mirror}] < {\rm maxRight} - i$, which means that ${\rm P}[i] = {\rm P}[{\rm mirror}]$.
- case 1: $i \ge {\rm maxRight}$
In summary, ${\rm P}[i] = \min\{ {\rm maxRight} - i, {\rm P}[{\rm mirror}] \}$.
1 | string manacher(string str) { |